Tìm hiểu về Angle Là Gì ?

[chuonggoiphucvu]

Angle : có nghĩa là góc

I. Giới thiệu về góc và đơn vị đo góc:​

Góc là một khái niệm cơ bản trong toán học và hình học, đại diện cho sự giao nhau của hai đoạn thẳng hoặc hai mặt phẳng tại một điểm chung, được gọi là đỉnh của góc. Để hiểu rõ hơn về góc, chúng ta cần tìm hiểu về đơn vị đo góc, vì góc được xác định bởi độ lớn của nó.

A. Khái niệm góc và đỉnh của góc:

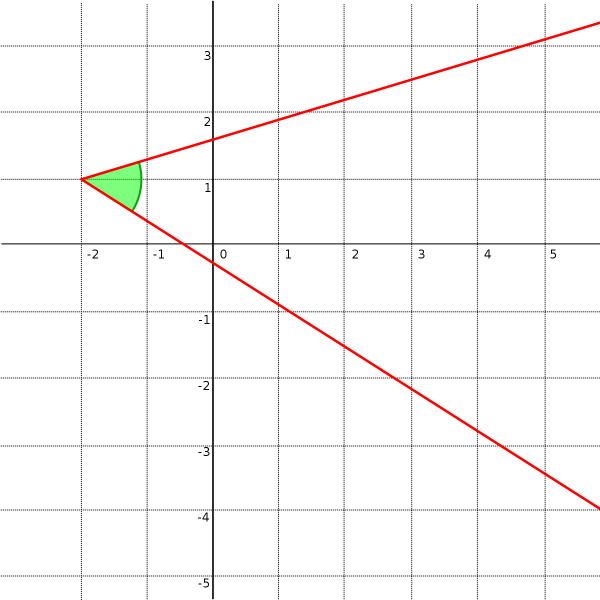
1. Góc:
   Trong mặt phẳng hai chiều, góc được tạo thành bởi hai tia (đoạn thẳng có một đầu điểm chung) với điểm chung tạo thành đỉnh. Góc được ký hiệu bằng các chữ cái, thường là ba chữ cái viết liền nhau tại đỉnh góc (ví dụ: ∠ABC).
2. Đỉnh:
   Đỉnh của góc là điểm chung giữa hai tia hoặc hai mặt phẳng tạo thành góc.

B. Đơn vị đo góc phổ biến: độ và radian:

1. Độ (degrees):
   Đây là đơn vị đo góc phổ biến và thường gặp trong cuộc sống hàng ngày. Một vòng tròn được chia thành 360 độ, và mỗi độ được chia thành 60 phút và mỗi phút chia thành 60 giây.
2. Radian (radians):
   Radian là một đơn vị đo góc khác, phổ biến trong các ứng dụng toán học và khoa học. Nó đo lường góc bằng cách sử dụng bán kính vòng tròn. Một vòng tròn đầy đủ có 2π radian, tương đương với 360 độ. Vì vậy, một góc vuông đo bằng radian là π/2 radian.

Việc sử dụng đơn vị đo góc phù hợp là tùy thuộc vào ngữ cảnh và ứng dụng của bài toán. Trong các tình huống hàng ngày, độ là đơn vị phổ biến và dễ hiểu. Trong khi đó, radian thường được sử dụng trong các bài toán toán học phức tạp và tính toán khoa học. Hiểu và sử dụng đúng đơn vị đo góc là cần thiết để giải quyết các bài toán và ứng dụng thực tế liên quan đến góc trong cuộc sống hàng ngày.

II. Cách đo góc và góc đặc biệt trong hình học:​

A. Phương pháp đo góc sử dụng thước góc và các công cụ khác:

1. Thước góc:
   
   
   
   Thước góc là công cụ đo góc thông dụng nhất và dễ sử dụng. Nó được làm từ kim loại hoặc nhựa, có một đầu đặt lên đỉnh góc và một vạch chia ghi đoạn thẳng. Bằng cách đặt thước góc trên các cạnh của góc cần đo, ta có thể đọc giá trị góc trên vạch chia để xác định độ lớn của góc đó.
2. Bộ goniometer (gôn-i-ôm-ét):
   Là một công cụ đo góc chính xác hơn, thường được sử dụng trong nghiên cứu khoa học và công nghiệp. Nó có thể đo góc với độ chính xác cao và được sử dụng trong các ứng dụng y khoa, địa chất, và kỹ thuật.

B. Góc vuông, góc tù, và góc nhọn:

1. Góc vuông:
   Góc vuông là góc có kích thước bằng chính xác 90 độ. Đây là góc quan trọng trong hình học và trong cuộc sống hàng ngày, vì nó đại diện cho góc đứng thẳng và thường được sử dụng trong kiến trúc, xây dựng và cơ khí.
2. Góc tù:
   Góc tù là góc có kích thước lớn hơn 90 độ và nhỏ hơn 180 độ. Nó là một góc mở hơn góc vuông và có ứng dụng trong việc xác định các góc nhọn trong các hình học phức tạp.
3. Góc nhọn:
   Góc nhọn là góc có kích thước nhỏ hơn 90 độ. Góc nhọn cũng có nhiều ứng dụng trong cuộc sống hàng ngày và trong nhiều lĩnh vực khoa học và kỹ thuật.

Hiểu về cách đo góc và các loại góc đặc biệt là rất quan trọng trong hình học và các ứng dụng của nó trong cuộc sống hàng ngày. Việc đo và xác định các góc giúp ta giải quyết nhiều bài toán thực tế, từ định hướng trên bản đồ đến tính toán trong kiến trúc và xây dựng. Ngoài ra, các loại góc đặc biệt như góc vuông, góc tù và góc nhọn giúp ta xác định các đặc tính và tính chất của hình học và các đối tượng trong thế giới xung quanh chúng ta.

III. Ứng dụng của góc trong cuộc sống hàng ngày:​

A. Định hướng và đo góc trong bản đồ và hệ thống định vị GPS:

1. Định hướng:
   Góc được sử dụng để xác định hướng đi và vị trí trong bản đồ và bản đồ số. Khi chúng ta di chuyển từ một địa điểm đến địa điểm khác, chúng ta cần phải biết hướng và góc để xác định đường đi chính xác.
2. Hệ thống định vị GPS:
   Trong thiết bị định vị GPS, góc được sử dụng để xác định vị trí và hướng di chuyển của một người hoặc phương tiện di chuyển. Nhờ vào GPS, ta có thể dễ dàng xác định vị trí và định hướng trong điều kiện thời tiết và môi trường đa dạng.

B. Ứng dụng của góc trong thiết kế và xây dựng:

1. Kiến trúc:
   Góc được sử dụng trong thiết kế và xây dựng các công trình kiến trúc. Quyết định và tính toán các góc đảm bảo rằng các cấu trúc sẽ được xây dựng chính xác, vững chắc và hợp lý về thẩm mỹ.
2. Đo góc trong xây dựng:
   Công nhân xây dựng sử dụng thước góc và công cụ đo góc để đảm bảo độ chính xác của việc xây dựng các cấu trúc như tường, cửa, cột và mái.

C. Góc trong khoa học và công nghệ:

1. Điện tử và robot học:
   Trong khoa học điện tử và robot học, góc được sử dụng để điều khiển và định hướng các thiết bị tự động như robot, máy bay không người lái và các thiết bị tự động khác.
2. Truyền thông:
   Trong công nghệ truyền thông, góc được sử dụng để tối ưu hóa việc phát sóng và thu sóng trong các thiết bị điện thoại di động, sóng vô tuyến và các thiết bị truyền thông khác.

Góc là một yếu tố quan trọng và phổ biến trong nhiều khía cạnh của cuộc sống hàng ngày và trong nhiều lĩnh vực chuyên môn. Từ định hướng trong bản đồ đến xây dựng công trình, từ điều khiển robot đến truyền thông, hiểu biết và ứng dụng góc đóng một vai trò quan trọng trong việc giải quyết các vấn đề thực tế và phát triển các công nghệ tiên tiến.

IV. Góc trong các lĩnh vực chuyên môn:​

A. Góc trong vật lý và cơ học:

1. Động lực học:
   
   
   
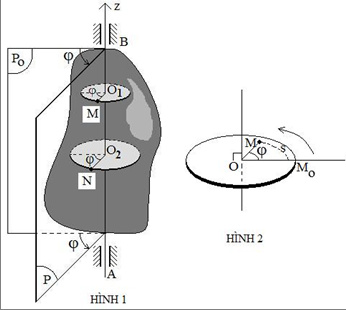
   Trong vật lý động học, góc được sử dụng để xác định chuyển động quay của các vật thể. Moment quán tính, quỹ đạo quay và tốc độ góc là những khái niệm quan trọng dựa trên góc trong vật lý.
2. Cân bằng và tính cứng của các vật thể:
   Góc được sử dụng để xác định cân bằng và tính cứng của các vật thể, đặc biệt trong các bài toán cơ học và kỹ thuật.

B. Góc trong hình học và hình học không gian:

1. Hình học tam giác và đa giác:
   Góc là một khái niệm cơ bản trong hình học tam giác và đa giác, được sử dụng để tính toán các đặc tính và thuộc tính của các hình học này.
2. Hình học không gian:
   Trong hình học không gian, góc được sử dụng để xác định sự vuông góc giữa các mặt phẳng, tính toán khoảng cách giữa các đoạn thẳng và giải quyết các bài toán không gian phức tạp.

C. Góc trong điện tử và máy tính:

1. Điện tử số:
   Trong viễn thông và điện tử số, góc được sử dụng để xác định pha của các tín hiệu và tín hiệu điều khiển trong các hệ thống truyền thông và xử lý số.
2. Đồ họa máy tính:
   Trong đồ họa máy tính, góc được sử dụng để xác định hướng nhìn của người dùng, phương diện ánh sáng và hiển thị 3D, giúp tạo ra các hình ảnh chân thực và sống động.

Góc đóng một vai trò quan trọng trong nhiều lĩnh vực chuyên môn, từ vật lý và cơ học đến hình học và hình học không gian, cũng như trong điện tử và máy tính. Hiểu biết về góc và cách áp dụng nó trong các lĩnh vực này giúp ta giải quyết các bài toán phức tạp và phát triển các công nghệ tiên tiến trong thế giới hiện đại.

Nguồn : https://chuonggoi.net/angle-la-gi/